Cet article illustre un exemple d’usage proposé par le GEP de l’académie de Versailles présentant quelques plus-values du numérique dans le cadre de mesures hors la classe.

Professeur expérimentateur

• Jean-Charles Moreau-Trouvé
• Lycée George-Sand – Domont (Val d’Oise)

Niveau - Thèmes

• Lycée
• Niveau : Première (enseignement de spécialité)
• Thème : Mouvements et interactions

Introduction

Cette activité expérimentale hors la classe se propose de mesurer à l’aide des capteurs présents dans un téléphone la pression de l’air et l’altitude, permettant ainsi de tester la loi fondamentale de la statique des fluides.
Les résultats expérimentaux sont ensuite exploités pour estimer la valeur de la masse volumique de l’air.
Une attention particulière est portée sur la prise en compte des incertitudes de mesure.

Contenus disciplinaires

• Notions et contenus :
  Grandeurs macroscopiques de description d’un fluide au repos : masse volumique, pression, température.
  Loi fondamentale de la statique des fluides.
• Compétences exigibles :
  Tester la loi fondamentale de la statique des fluides.
  Dans le cas d’un fluide incompressible au repos, utiliser la relation fournie exprimant la loi fondamentale de la statique des fluides : P₂ - P₁ = ρ·g·(z₁ - z₂)

Compétences

• S’APPROPRIER : S’approprier des documents et les données issues d’une application sur téléphone.
• ANALYSER : Proposer un protocole pour mener à bien l’étude expérimentale.
• RÉALISER : Représenter graphiquement des données de mesures ; Modéliser une série de mesures ; Déterminer le coefficient directeur d’une droite.
• VALIDER : Représenter graphiquement l’incertitude sur une mesure par des barres d’erreur ; Tester une loi en étudiant la correspondance entre données et modèle ; Estimer l’incertitude-type sur un résultat en prenant en compte les mesures de tous les groupes.
• COMMUNIQUER : Présenter correctement le résultat de la masse volumique de l’air.

CRCN – Compétences Numériques (Pix)

• 1.3. « Traiter des données » : Traiter des données pour analyser une problématique.
• 2.3. « Collaborer » : Utiliser un dispositif d’écriture collaborative.

Objectif(s) pédagogique(s)

• Utiliser le numérique pour réaliser des mesures hors la classe.
• Tester expérimentalement une loi physique.
• Ancrer la notion de régression linéaire.
• Évaluer la compatibilité d’un résultat expérimental avec une valeur de référence.

Objectifs disciplinaires et/ou transversaux

• Réaliser des mesures de pression et d’altitude en extérieur, en utilisant les capteurs d’un téléphone.
• Représenter graphiquement des valeurs expérimentales en tenant compte des incertitudes associées.
• Tester graphiquement la validité de la loi fondamentale de la statique des fluides.
• Estimer la valeur de la masse volumique de l’air à partir d’une série de mesures et comparer avec une valeur de référence.

Description de l’activité

Cette activité expérimentale a été testée en forêt de Montmorency, dans une zone interdite à la circulation et présentant un dénivelé d’une cinquantaine de mètres.

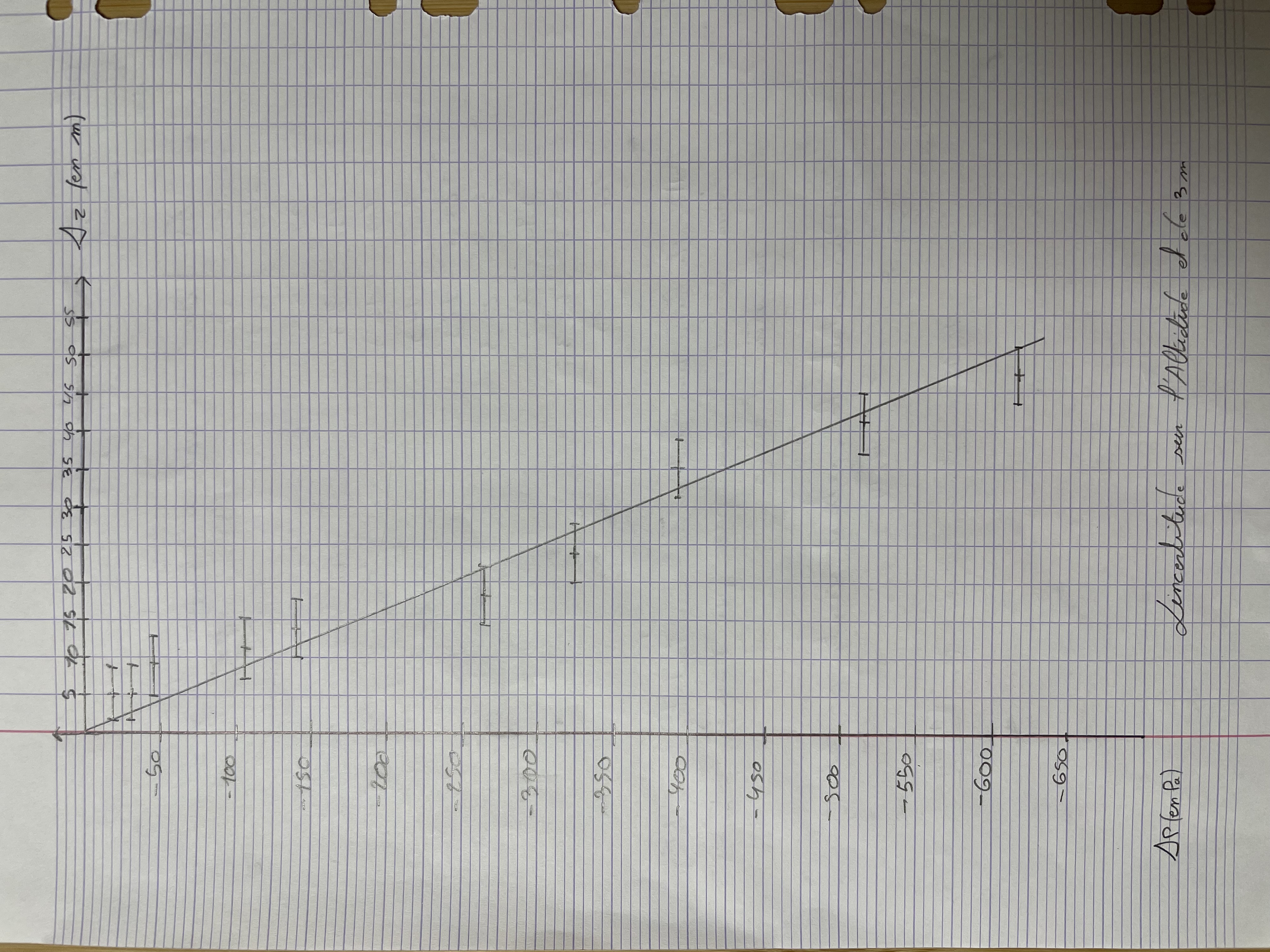
Chaque groupe d’élève a réalisé entre dix et vingt mesures d’altitude et de pression à l’aide de l’application Phyphox installée sur téléphone.
Le tracé de la variation de pression en fonction de la variation d’altitude a été réalisé manuellement, sur place.
La régression linéaire et la validation de la loi fondamentale de la statique des fluides ont également été réalisées sur place.

L’estimation de la masse volumique de l’air, la présentation du résultat de mesure à partir des résultats de tous les groupes et la discussion de la compatibilité du résultat avec une valeur de référence ont été traitées en classe.

Pré-requis

• Loi de la statique des fluides dans l’eau.
• Traitement statistique d’une série de mesures.

Outils utilisés – Matériel

• Application Phyphox disponible sous Android et iOS
• Alternative : application FizziQ disponible sous Android et iOS : plus conviviale, mais n’affichant pas l’incertitude sur la mesure d’altitude

Scénario pédagogique de la séquence

Le carnet de bord ci-dessous renseigne sur le scénario global. Il comprend toutes les activités et ressources (papiers ou numériques) proposées aux élèves :

Séance 1 (Partie 1)	Séance 1 (Partie 2)	Séance 2
Travail en extérieur	Travail en extérieur (possible en classe)	Travail en classe
1 heure	1 heure	1 heure
Objectifs visés : Réaliser une série de mesures de pression et d’altitude.	Objectifs visés : Exploiter la série de mesures pour tester graphiquement la loi de la statique des fluides.	Objectifs visés : Exploiter les représentations graphiques pour estimer la valeur de la masse volumique de l’air dans les conditions de l’expérience.
Descriptif des contenus et liens utiles : Lien vers l’activité	Descriptif des contenus et liens utiles : Lien vers l’activité	Descriptif des contenus et liens utiles : Lien vers l’activité
Liste des actions individuelles et/ou collectives : Réaliser une série de mesures de pression et d’altitude en se déplaçant sur le terrain expérimental. L’incertitude sur la pression est estimée grâce aux fluctuations de la valeur affichée, et celle de l’altitude est donnée par l’application.	Liste des actions individuelles et/ou collectives : Représenter graphiquement la variation de pression en fonction de la variation d’altitude, en traçant les barres d’incertitude. L’incertitude sur la pression étant très faible comparativement à la valeur mesurée, elle n’apparaît pas sur la représentation graphique. Modéliser (si possible) la série de points par une droite passant par l’origine, comme le prévoit la loi fondamentale de la statique des fluides. Conclure sur la validité de la loi dans les conditions de l’expérience.	Liste des actions individuelles et/ou collectives : À partir de la régression linéaire proposée, déterminer la valeur du coefficient directeur puis en déduire une estimation de la masse volumique de l’air dans les conditions de l’expérience. Exploiter les résultats de tous les groupes de la classe pour déterminer la moyenne et l’incertitude-type de la mesure de la masse volumique de l’air. Présenter le résultat de l’expérience et conclure sur sa compatibilité avec la valeur de référence.
Liste des actions d’encadrement : Vérifier que les élèves exploitent correctement le terrain expérimental (dénivelé important). Si nécessaire, guider les élèves pour la détermination de l’incertitude sur les deux grandeurs mesurées.	Liste des actions d’encadrement : Si nécessaire, préciser aux élèves que la régression linéaire est validée s’il est possible de faire passer une droite par l’ensemble des barres d’incertitude.	Liste des actions d’encadrement : Si nécessaire, rappeler aux élèves la méthode pour déterminer un coefficient directeur. Proposer une phrase type de conclusion sur la présentation du résultat de mesure de la masse volumique de l’air dans les conditions de l’expérience.

Retour d’expérience

Les plus-values pédagogiques (enseignants / élèves)

Les plus values pour la discipline

• L’expérimentation hors du laboratoire permet de proposer un cadre expérimental très concret aux élèves, ancré dans le réel, sans faire appel à du matériel de laboratoire didactisé.
• La mesure sur le terrain permet de donner davantage de sens aux variations d’altitude et donc de pression : les écarts sont plus importants.
• Le travail sur les barres d’incertitudes a permis aux élèves de mieux appréhender la notion de régression linéaire : tracé d’une droite passant au mieux par toutes les barres d’incertitude.
• Le travail sur les barres d’incertitudes a permis aux élèves de mieux appréhender la notion de modèle : le modèle est validé si une droite passant par toutes les barres d’incertitudes peut être tracée, et invalidée sinon.
• Les multiples mesures permettent de réactiver les notions (travaillées dans d’autres contextes) d’incertitude-type, de présentation d’un résultat et de compatibilité avec une valeur de référence.

Les points de vigilance

• Il est nécessaire de choisir un lieu possédant un dénivelé important (environ 50 m ici) et où un signal GPS suffisant peut être capté.
• Si l’incertitude sur la mesure de l’altitude est donnée par l’application, celle sur la mesure de pression est à estimer à partir des fluctuations des derniers digits de la valeur affichée en un point donné. Ici, les élèves ont estimé l’incertitude sur la pression à 1 bar ou 10 bar.
• Si l’incertitude sur la pression n’est pas négligeable par rapport à la valeur mesurée, on représentera des rectangles d’incertitude et non des barres d’incertitude.
• Certains élèves ont rencontré des difficultés pour calculer les variations ΔP et Δz de pression et d’altitude. Une aide ponctuelle a permis de les aiguiller.
• Quelques élèves ne savaient plus déterminer un coefficient directeur. Une aide ponctuelle a permis de les aiguiller.

Les pistes pour aller plus loin ou généraliser la démarche

• Dans une zone montagneuse où de forts dénivelés sont accessibles (de l’ordre de 1000 m), il est envisageable de montrer l’écart à la linéarité entre la variation de pression et la variation d’altitude, la masse volumique ne pouvant plus être considérée comme constante sur de tels dénivelés.
• Une autre approche de l’évaluation des incertitudes de mesure consiste à déterminer l’incertitude-type sur le coefficient directeur (et sur l’ordonnée à l’origine) de la droite représentant ΔP en fonction de Δz. Il faut pour cela calculer le résidu pour chaque point, puis calculer l’écart-type statistique qui quantifie la dispersion des points expérimentaux par rapport au modèle linéaire. Ce traitement peut se faire à l’aide d’un langage de programmation (Python par exemple).